Круги эйлера примеры по рисунку. Использование метода кругов Эйлера (диаграмм Эйлера–Венна) при решении задач в курсе информатики и ИКТ. Задача про любимые мультфильмы

Не потеряйте. Подпишитесь и получите ссылку на статью себе на почту.

Круги Эйлера представляют собой особую геометрическую схему, необходимую для поиска и более наглядного отображения логических связей между понятиями и явлениями, а также для изображения отношений между определенным множеством и его частью. Благодаря наглядности они значительно упрощают любые рассуждения и помогают быстрее находить ответы на вопросы.

Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. С момента своего появления метод приобрел широкую популярность и признание.

Леонард Эйлер – российский, немецкий и швейцарский математик и механик. Внес огромный вклад в развитие математики, механики, астрономии и физики, а также ряда прикладных наук. Написал больше 850 научных работ по теории чисел, теории музыки, небесной механике, оптике, баллистике и другим направлениям. Среди этих работ несколько десятков фундаментальных монографий. Половину жизни Эйлер прожил в России и оказал большое влияние на становление российской науки. Многие его труды написаны на русском языке.

Позже круги Эйлера использовали в своих работах многие известные ученые, к примеру, чешский математик Бернард Больцано, немецкий математик Эрнест Шредер, английский философ и логик Джон Венн и другие. Сегодня методика служит основной многих упражнений на развитие мышления, в том числе и упражнений из нашей бесплатной онлайн-программы « ».

Для чего нужны круги Эйлера

Круги Эйлера имеют прикладное значение, ведь с их помощью можно решать множество практических задач на пересечение или объединение множеств в логике, математике, менеджменте, информатике, статистике и т.д. Полезны они и в жизни, т.к., работая с ними, можно получать ответы на многие важные вопросы, находить массу логических взаимосвязей.

Есть несколько групп кругов Эйлера:

равнозначные круги (рисунок 1 на схеме);
пересекающиеся круги (рисунок 2 на схеме);
подчиненные круги (рисунок 3 на схеме);
соподчиненные круги (рисунок 4 на схеме);
противоречащие круги (рисунок 5 на схеме);
противоположные круги (рисунок 6 на схеме).

Посмотрите схему:

Но в упражнениях на развитие мышления чаще всего встречаются два вида кругов:

Круги, описывающие объединения понятий и демонстрирующие вложенность одного в другое. Посмотрите пример:

Круги, описывающие пересечения разных множеств, имеющих некоторые общие признаки. Посмотрите пример:

Результат использования кругов Эйлера проследить на этом примере очень просто: обдумывая, какую профессию выбрать, вы можете либо долго рассуждать, пытаясь понять, что больше подойдет, а можете нарисовать аналогичную диаграмму, ответить на вопросы и сделать логический вывод.

Применять метод очень просто. Также его можно назвать универсальным – подходящим для людей всех возрастов: от детей дошкольного возраста (в детских садах детям преподают круги, начиная с 4-5-летнего возраста) до студентов (задачи с кругами есть, к примеру, в тестах ЕГЭ по информатике) и ученых (круги широко применяются в академической среде).

Типичный пример кругов Эйлера

Чтобы вы могли лучше понять, как «работают» круги Эйлера, рекомендуем познакомиться с типичным примером. Обратите внимание на нижеследующий рисунок:

На рисунке зеленым цветов отмечено наибольшее множество, представляющее собой все варианты игрушек. Один из них – это конструкторы (голубой овал). Конструкторы – это отдельное множество само по себе, но в то же время и часть общего множества игрушек.

Заводные игрушки (фиолетовый овал) тоже относятся к множеству игрушек, однако к множеству конструктора они отношения не имеют. Зато заводной автомобиль (желтый овал), пусть и является самостоятельным явлением, но считается одним из подмножеств заводных игрушек.

По подобной схеме строятся и решаются многие задачи (включая и задания на развитие когнитивных способностей), задействующие круги Эйлера. Давайте разберем одну такую задачу (кстати, именно ее в 2011 году внесли на демонстрационный тест ЕГЭ по информатике и ИКТ).

Пример решения задачи с помощью кругов Эйлера

Условия задачи таковы: приведенная таблица показывает, сколько страниц было найдено в Интернете по конкретным запросам:

Вопрос задачи: сколько страниц (в тысячах) выдаст поисковик по запросу «Крейсер и линкор»? При этом нужно учитывать, что все запросы выполняются примерно в одно и то же время, поэтому набор страниц с искомыми словами со времени выполнения запросов остался неизменным.

Решается задача так: с помощью кругов Эйлера изображаются условия задачи, а цифрами «1», «2» и «3» обозначаются полученные в результате сегменты:

Учитывая условия задачи, составляем уравнения:

Крейсер/линкор: 1+2+3 = 7 000;
Крейсер: 1+2 = 4 800;
Линкор: 2+3 = 4 500.

Чтобы определить количество запросов «Крейсер и линкор» (сегмент обозначен цифрой «2» на рисунке), подставим в уравнение 1 уравнение 2 и получим:

4 800 + 3 = 7 000, а значит, что 3 = 2 200 (т.к. 7 000-4 800 = 2 200).

2 + 2 200 = 4 500, а это означает, что 2 = 2 300 (т.к. 4 500-2 200 = 2 300).

Ответ: по запросу «Крейсер и линкор» будет найдено 2 300 страниц.

Этот пример наглядно демонстрирует, что с помощью кругов Эйлера можно достаточно быстро и просто решать сложные задачи.

Резюме

Круги Эйлера – это очень полезная методика решения задач и установления логических связей, а заодно и занимательный и интересный способ провести время и потренировать мозг. Так что, если вам хочется совместить приятное с полезным и поработать головой, предлагаем пройти наш курс « », включающий в себя самые разные задания, в том числе и круги Эйлера, эффективность которых научно обоснована и подтверждена многолетней практикой.

Решение логических задач с помощью кругов Эйлера

Круги Эйлера – задачи на пересечение или объединение множеств Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.

Круги Эйлера - геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.

Задача 1. В классе 35 учеников. Из них 20 человек занимаются в математическом кружке, 11 - в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?

Изобразим эти кружки на рисунке. Можем, например, начертить в школьном дворе большой круг, а в нем два поменьше. В левый круг, обозначенный буквой М, поместим всех математиков, а в правый, обозначенный буквой Б, всех биологов. Очевидно, в общей части кругов, обозначенной буквами МБ, окажутся те самые биологи-математики, которые нас интересуют. Остальных ребят класса, а их 10, попросим не выходить из внешнего круга, самого большого. Теперь посчитаем: всего внутри большого круга 35 ребят, внутри двух меньших 35 - 10 = 25 ребят. Внутри «математического» круга М находятся 20 ребят, значит, в той части «биологического» круга, которая расположена вне круга М, находятся 25 - 20 = 5 биологов, не посещающих математический кружок. Остальные биологи, их 11 - 5= = 6 человек, находятся в общей части кругов МБ. Таким образом, 6 биологов увлекаются математикой.

Задача 2. .В классе 38 человек. Из них 16 играют в баскетбол , 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом.

Сколько ребят увлекаются одновременно тремя видами спорта?

Сколько ребят увлекается лишь одним из этих видов спорта?

Решение. Воспользуемся кругами Эйлера. Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта - баскетболом занимаются 16 - (4 + z + 3) = 9 - z; одним лишь хоккеи 17 - (4 + z + 5) = 8 - z;

одним лишь футболом 18 - (3 + z + 5) = 10 - z.

Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам:

3 + (9 - z) + (8 - z) + (10 - z) + 4 + 3 + 5 + z = 38,

Таким образом, двое ребят увлекаются всеми тремя видами спорта.

Складывая числа 9 - z, 8 - z и 10 - z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек.

Двое ребят увлекаются всеми тремя видами спорта человека.

Увлекающихся лишь одним видом спорта: 21 человек.

Задача 3 . Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».

11 – 6 = 5 – человек, которые смотрели только «Стиляги».

Получаем:

Ответ. 5 человек смотрели только «Стиляги».

Задача 4. Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?

В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Получаем:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.

Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».

Задача 5 . В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?

Изобразим эти множества на кругах Эйлера.

Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:

Ответ: 6 покупателей купили диски и Максим, и Земфиры.

Задача 6 . На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. прочитал 11 книг. Сколько книг прочитал Рон?

Учитывая условия задачи, чертеж будет таков:

https://pandia.ru/text/80/398/images/image010_1.jpg" alt="22.PNG" width="243" height="158">

70 – (6 + 8 + 10 + 3 + 13 + 6 + 5) = 19 – ребят не поют, не увлекаются спортом, не занимаются в драмкружке. Только спортом заняты 5 человек.

Ответ. 5 человек заняты только спортом.

Задача 8. Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.

Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.

Министерство образования, науки и молодежи Республики Крым Малая академия наук «Искатель»

Направление: математика

г. Красноперекопск – 2017

Работу выполнила:

Шумилина Мария Сергеевна,

ученица 7-А класса муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная школа № 5» муниципального образования городской округ Красноперекопск

Научный руководитель:

Шеина Елена Николаевна, учитель математики муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная школа № 5 » муниципального образования городской округ Красноперекопск

ВВЕДЕНИЕ …………………………………………………………… 3

ГЛАВА 1. Немного из истории…………………………………. 5

ГЛАВА 2. Из теории множеств……………………………………….7

2.1. Понятие множества.……………………………………..8

2.2. Операции над множествами. …………………………..9

ГЛАВА 3. Решение задач с помощью кругов Эйлера ………………..10

ЗАКЛЮЧЕНИЕ…………………………………………………………..22

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ………………….23

ВВЕДЕНИЕ

Ничто так не способствует

формированию мыслительной культуры,

как решение логических задач. Математика-

не сухая и скучная наука, а полная

необычных и интересных открытий

Решать логические задачи очень увлекательно. Есть люди, для которых решение логической задачи - увлекательная, но несложная задача. Их мозг как луч прожектора сразу освещает все хитроумные построения, и к правильному ответу они приходят необычайно быстро. Замечательно, что при этом не могут объяснить, как пришли к решению.

Логические задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде, всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам.

Существует множество приемов, которые используются при решении текстовых логических задач. Очень часто решение помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению.

Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь.

Цель работы:

Познакомится с кругами Эйлера – Венна;

Научиться применять способ решения задач с помощью кругов Эйлера;

Составлять задачи практического содержания.

Глава 1. Немного из истории

Леонард Эйлер, крупнейший математик XVIII в., родился в Швейцарии в 1707г. В 1727 г. по приглашению Петербургской академии наук он приехал в Россию. В Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков, астрономов, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира. Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома. Среди его работ - первые учебники по дифференциальному и интегральному исчислению. В теории чисел Эйлер продолжил деятельность французского математика П. Ферма.

Эйлер много работает в области математического анализа. Ученый впервые разработал общее учение о логарифмической функции. В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку-топологию.

Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В -Р + Г = 2. Даже основные результаты научной деятельности Эйлера трудно перечислить. Здесь и геометрия кривых и поверхностей, и первое изложение вариационного исчисления с многочисленными новыми конкретными результатами. У него были труды по гидравлике, кораблестроению, артиллерии, геометрической оптике и даже по теории музыки. Он впервые дает аналитическое изложение механики вместо геометрического изложения Ньютона, строит механику твердого тела, а не только материальной точки или твердой пластины. Одно из самых замечательных достижений Эйлера связано с астрономией и небесной механикой. Он построил точную теорию движения Луны с учетом притяжения не только Земли, но и Солнца. Это пример решения очень трудной задачи.

Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него наиболее громоздкие вычисления.

С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения».

После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

Глава 2. Из теории множеств

2.1. Понятие множества.

Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты – элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы – ученики),множестве дней недели (элементы – дни недели), множестве натуральных делителей числа 6 (элементы – числа 1, 2, 3, 6) и т. д.

В курсах алгебры и алгебры начало анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.

Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество M состоит из чисел 1; 2; 3, то его обозначают так: M = {1; 2; 3}. Тот факт, что число 2 входит в это множество

(является элементом данного множества M ) записывается с помощью специального значка следующим образом: 2 M ; а то что число 5 не входит в это множество (не является элементом данного множества M ), записывается так: 5 M .

Можно рассматривать также множество, не содержащее ни одного элемента, - пустое множество. Например: множество простых делителей числа 1 – пустое множество.

Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом , множество всех натуральных чисел – буквой N , множество всех целых чисел – буквой Z , множество всех рациональных чисел – буквой Q , а множество всех действительных чисел буквой R . С помощью кругов Эйлера – Венна это можно изобразить так:

Рис.1

Если каждый элемент множества A является элементом множества B , то говорят, что множество A является подмножеством множества B .

Это записывают следующим образом: A B .

Рис.2

2.2. Операции над множествами.

Над множествами можно выполнять определенные действия: находить их пересечение, объединение. Дадим определение этих операций и проиллюстрируем их с помощью кругов.

Пересечением множеств A и B называют их общую часть, то есть множество C всех элементов, принадлежащих как множеству A , так и множеству B

Пересечение множеств обозначают знаком ∩ и записывают A ∩ B .

Рис.3

Объединением множеств A и B называют множество C , состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств (A или B ). Объединение множеств обозначают знаком
и записывают A
B

Глава3. Решение задач с помощью Кругов Эйлера

Задача № 1.

Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 - и значки, и марки.

Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием.

Решение.

В условии этой задачи не так легко разобраться. Если сложить 23 и 35, то получится больше 52. Это объясняется тем, что некоторых школьников мы здесь учли дважды, а именно тех, которые собирают и значки, и марки.

чтобы легче решать задачу, представим ее данные на следующей схеме

Рис.5

На этой схеме большой круг означает всех школьников, о которых идёт речь. Круг З изображает школьников, собирающих значки (всего их 23), а круг М - школьников, собирающих марки (всего их 35). В пересечении кругов З и М стоит число 16 - это те, кто собирает и значки, и марки. Значит, только значки собирает 23 - 16 = 7 человек, только марки собирает 35 - 16 = 19 человек. Всего марки и значкисобирает19 + 7 + 16 = 42 человека. Остаётся 52 - 42 = 10 человек, не увлечённых коллекционированием. Это число можно вписать в свободное поле круга. Ответ: 10 человек.

Задача 2.

В классе 15 мальчиков. Из них 10 человек занимается волейболом и 9 баскетболом. Сколько мальчиков занимается и тем, и другим?

Решение.

Изобразим условие с помощью кругов Эйлера. Этот рисунок подсказывает нам рассуждения. Разберём это рассуждение и впишем нужное число в каждую из образовавшихся на диаграмме частей.

Пусть всеми видами спорта занимаются х мальчиков. Тогда только волейболом занимаются (10-х) мальчиков, а только баскетболом (9-х) мальчиков. Составим уравнение: 10-х + х+ 9-х=15, откуда х=4

10-х Б

х 9-х

Рис.6

Ответ: 4 человека.

Задача № 3.

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Чучело», 11 человек – фильм «Выше неба», из них 6 смотрели и «Чучело», и «Выше неба». Сколько человек смотрели только фильм «Выше неба»?

Решение: Чертим два множества таким образом: 6 человек, которые смотрели фильмы «Чучело» и «Выше неба», помещаем в пересечение множеств.

15 – 6 = 9 – человек, которые смотрели только «Чучело».
11 – 6 = 5 – человек, которые смотрели только «Выше неба».

Получаем:

Рис.7

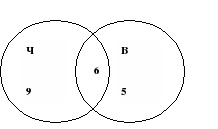
Ответ. 5 человек смотрели только «Выше неба».

Задача № 4.

В группе из 80 туристов, приехавших на экскурсию в Москву, 52 хотят посетить Большой театр, 30 - Художественный театр, 12 хотят посетить оба театра, остальные в театры ходить не хотят. Сколько человек не собирается идти в театр?

Решение.

Только большой театр посетят: 52-12=40 туристов;

только художественный театр посетят

30-12=18 туристов;

8
0-(40+18+12)=10 туристов не собираются идти в театр.

Рис.8

Ответ: 10 человек.

Задача № 5.

На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?

Решение.

Учитывая условия задачи, чертеж будет таков:

Рис.9

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри.

Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон. Ответ. 8 книг прочитал Рон.

Задача№6.

В туристической группе из 100 человек 75 человек знают немецкий язык, 65 человек - английский язык, а 10 человек - не знают ни немецкого, ни английского языка. Сколько туристов знают два языка? Решение.

Изобразим условие задачи в виде кругов Эйлера.

Легко видеть, что 90 туристов (100-10) знают хотя бы один язык; Пусть х туристов знают и английский, и немецкий языки. Тогда (65-х) туристов знают только английскй, а (75-х) человек только немецкий. Получим уравнение 65-х+75-х+х=90, откуда х=50 – туристов знают оба языка. Ответ: 50 туристов.

Задача№7.

Сколько человек участвует в прогулке, если известно, что 16 из них взяли бутерброд с ветчиной, 24 - с колбасой, 15 - с сыром, 11 и с ветчиной, и с колбасой, 8 и с ветчиной, и с сыром, 12 и с колбасой, и с сыром, 6-бутерброды всех видов, а 5- взяли пирожки? Решение : Изобразим множества следующим образом: Рис.11

16+24+15-11-8-12+6=30(чел) - участвовали в прогулке и с собой брали бутерброды или 3+2+6+5+7+6+1=30(чел)

30+5=35(чел) - участвовали в прогулке
Ответ. 35 человек

Задача №8

В 5 классе нашей школы 22, в 6 классе – 16, в 7 классе – 23 ребят. Известно, что кружки по лыжам, шахматам и спортивным играм ходят 4 человека. Каждые две секции посещают 9 человек. Сколько человек ходит из каждого класса на секции? Сколько учеников не ходит ни на какой спортивный кружок?

Решение. Если на все три кружка ходят 4 ученика, а на каждые два – 9 человек, то две секции с 5 и 6 класса, с 6 и 7 класса, с 5 и 7 класса посещают по 5

человек.

Рис.12

Получаем 5+5+4=14 пятиклассников посещают кружки, 22-14=8 человек не ходят ни на какой кружков. Рассуждая также, из шестиклассников 16-14=2 ученика никуда не ходя, а из семиклассников – 23-14=9 человек.

Ответ: 14 учеников с каждого класса посещают кружки, не ходят ни на какой из 5-ого – 7, из 6-ого – 2, из 7-ого – 9 учеников.

Задача № 9.

Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

Решение: В оспользуемся кругами Эйлера.

Рис.13

Задача № 10 .

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение . Д - драмкружок; Х - хор; С - спорт. В круге Д - 27 ребят, в круге Х - 32 человека, в круге С - 22 ученика. Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8-3=5

спортсменов, не поющих в хоре и 6-3=3, не посещающих драмкружок. Легко видеть, что 5+3+3=11 спортсменов посещают хор или драмкружок, 22-(5+3+3)=11 заняты только спортом; 70-(11+12+19+7+3+3+5)=10 - не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

Рис.14 Ответ: 10 человек.

Задача№11 . В классе 30 человек. 20 из них каждый день пользуются метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?

Решение.

Рис.15

Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом - (10 − х) человек, только автобусом и троллейбусом - (9 − х) человек, только метро и автобусом -(12 − х) человек. Найдем, сколько человек пользуется одним только метро:

20 − (12 − х) − (10 − х) − х = х − 2

Аналогично получаем: х − 6 - только автобусом и х + 4 - только троллейбусом, так как всего 30 человек, составляем уравнение:

х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30.

отсюда х = 3.

Ответ: 3 человека.

Задача № 12.

Из сотрудников фирмы 16 побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и Франции -6; во всех трех странах - 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Решение:

Нам известно, что во всех трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В Франции и Италии нам неизвестно поэтому пишем х-5 в пересечении кругов А и Ф. Т.к. в Англии было 6 человек, то 6-5-1=0 пишем 0,во Франции 16-х+5-6 и Италии 10-х+5-5 и всего в фирме 19 сотрудников, то остается составить и решить уравнение: 1+16-х+5-6+5+х-5+10-х+5-5=19, отсюда х=7, значит в Италии и Франции побывало 7-5=2 сотрудника фирмы.

Рис.16

Ответ: 2 сотрудника.

Задача № 13.

Ребят, которые хотят обмениваться различного рода журналами, собралось 10 человек. Среди них выписывают К - 6 человек, Т – 5 человек, Ю – 5 человек, К и Т – 3 человека, Т и Ю -2 человека, К и Ю – 3 человека., а один человек не выписывает ни одного журнала., но читает все эти журналы в библиотеке. Надо узнать, сколько человек выписывают все три журнала, сколько – два, а сколько – только один журнал.

Решение. Пусть большой круг, состоящий из 10 человек, – это множество всех ребят, обменивающихся журналами. Внутри большого круга нарисуем три меньших круга: К, Т, Ю, которые изображают ребят, подписавшихся на соответствующие журналы.. Известно, что один человек не выписывает ни одного журнала.

Пусть х ребят выписывают все три журнала, тогда (3-х)ребят выписывают только К и Т, (2-х) –только Т и Ю, (3-х)- только К и Ю. Значит, только журнал К выписывают 6-(3-х+х+3-х)=х человек, журнал Т 5-(3-х+х+2-х)=х, журнал Ю 5-(3-х+х+2-х)=х.

Рис.17

Составим уравнение: х+3-х+3-х+х+х+х+х+2-х=9, 8+х=9,х=1

Итак, 3 – это число ребят, подписавшихся только на один журнал, 5 – это число ребят, подписавшихся на два журнала, а 1 – число ребят, подписавшихся на все три журнала.

ЗАКЛЮЧЕНИЕ

Предмет математики настолько серьезен,

что нельзя упускать случая сделать

его немного занимательным.

Б. Паскаль

Среди математических задач логические задачи занимают особое место Решение таких задач способствует развитию математического мышления. Они отличаются от большинства математических задач тем, что для их решения часто не требуется запас каких-то специальных знаний, а нужна, как правило, сообразительность. Одна из характерных черт любой логики состоит в том, что она позволяет, получив некоторую информацию, извлечь (выявить) содержащиеся в ней новые знания.

Оказывается приемов, с помощью которых можно решать текстовые логические задачи, несколько. Они разнообразны и каждый из них имеет свою область применения.

В моей работе рассмотрены задачи, которые состоят из множества данных. Найденные решения подчиняются одному и тому же способу: составляем рисунок; заносим первоначальные данные в круги; анализируя и рассуждая, записываем результаты в части кругов; ищем и записываем ответ. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению. Кроме того с их помощью можно ответить на множество вопросов, поставленных к одному условию задачи.

Данная тема расширила мой математический кругозор, обогатила арсенал средств, используемых в решении разнообразных задач.

Список используемых источников:

1. Гаврилова Т. Д..Занимательная математика. 5 - 11 классы. Волгоград: Учитель, 2005.-96 с.

2. Германович П.Ю. «Сборник задач по математике на сообразительность».

3. Гетманова А. Д. Логические основы математики 10 – 11 класс: учебное пособие. – М.: Дрофа, 2005.

4. Глейзер Г. И. . - М.: Просвещение, 1964. - С. 232.

5. Гусев В.А., Орлов А.И., Розенталь А.Л. «Внеклассная работа по математике». М.: Просвещение, 1984.

6. Нелин Е.П., Долгова О.Е.. Учебник алгебра и начала анализа 11 класс.

Тезисы к работе

Тема моей исследовательской работы «Решение задач с помощью кругов Эйлера ». При подготовке к олимпиаде я столкнулась с задачами, в которых большое количество данных. Оказывается, упростить решение таких задач помогают так называемые круги Эйлера, с помощью которых можно изобразить множество элементов, обладающих определённым свойством. Целью данной работы является изучение этого способа и умение применять его для решения задач.

В работе рассмотрены задачи, решение которых подчиняются одному алгоритму: составляем рисунок; заносим первоначальные данные в круги, начиная с условия которое содержит больше свойств; анализируя и рассуждая записываем результаты в части круга; записываем ответ.

Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь. Способ, рассмотренный в работе доступен и легок в понимании, что позволяет расширить круг его применения. Круги Эйлера можно встретить и в истории, и в биологии, и при изучении других предметов.

Материал,который был исследован в работе,а также практическая часть, могут быть применены на дополнительных занятиях, при подготовке к математическим олимпиадам.

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

В наше время вокруг нас собрано огромное количества информации, разобраться в ней бывает непросто. Поэтому многие не знают, что за названием «Круги Эйлера» скрывается практичный и удобный метод решения различных задач. Все слышали о них, но немногие могут объяснить, что это такое. Однако я считаю, что Круги Эйлера полезны как в повседневной жизни, так и в науке, поэтому ими стоит уметь пользоваться каждому. В этой работе я собрала всю необходимую информацию для понимания, что такое Круги Эйлера и где их удобно применять.

Круги Эйлера — это геометрическая схема, с помощью которой можно наглядно изобразить отношения между различными множествами и подмножествами. Такая схема помогает находить логические связи между явлениями и понятиями, она изобретена Леонардом Эйлером, используется в математике и других научных дисциплинах. Использование Кругов Эйлера упрощает рассуждения и помогает быстрее и проще получить ответ. (1),(2)

Круги Эйлера неотрывно связаны с понятием множества. Поэтому, чтобы лучше понимать, что изображено на кругах Эйлера, нужно знать, что такое множество и какие множества бывают.

Под множеством можно понимать совокупность каких-либо объектов, называемых элементами множества. Во множества можно объединять любые объекты с общим признаком. Например, множество учеников гимназии 11, учащихся в 7 «Б» классе составляют отдельное множество. Множества могут быть и неодушевленных предметов. Например, множество книг, написанных каким-либо автором. С помощью кругов Эйлера множество обозначается, как пустой круг, а входящие в него элементы - точками. (5)

Давайте изобразим множество цифр. На рисунке контуром обозначено множество, а точками элементы этого множества.

Множества бывают трех видов:

· Конечное (например - множество цифр)

· Бесконечное (например - множество чисел)

· Пустое (множество натуральных чисел

меньше нуля). (5)

Группа предметов, образующая множество, входящее в состав более обширного множества, изображается в виде меньшего круга, нарисованного внутри большего круга, и называется подмножеством. Такое отношение образуется между большим множеством животных и входящим в его состав подмножеством плоских червей. (5)

В тех случаях, когда два понятия совпадают только частично, отношение между такими множествами изображается с помощью двух перекрещивающихся кругов. Такое отношение образуется между множеством учащихся 7 «Б» класса и множество троечников. Некоторые элементы множества учеников 7 «Б» класса принадлежат и к множеству троечников. (5)

Когда ни один предмет, из одного множества, не может одновременно принадлежать второму множеству, то отношение между ними изображается посредством двух кругов, нарисованных один вне другого. Такими множествами являются множество отрицательных и множество положительных чисел. (5)

Круги Эйлера были изобретены и названы в честь Леона́рда Э́йлера (портрет слева). Это был швейцарский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Эйлер родился в Швейцарии, учился в Германии, но работал и умер в России. Этот ученый - автор 800 работ. Леонард Эйлер родился в 1707 году в семье пастора. Его отец был другом семьи Бернулли. У Эйлера рано проявились математические способности. Обучаясь в гимназии, мальчик увлечённо занимался математикой, а позже стал посещать университетские лекции Иоганна Бернулли. 20 октября 1720 года Леонард Эйлер стал студентом факультета искусств Базельского университета. Одаренный молодой человек обратил на себя внимание профессора Иоганна Бернулли. Он передал студенту математические статьи для изучения, а также пригласил приходить к нему домой, чтобы совместно разбирать непонятное. В доме своего учителя Эйлер встретился и начал общаться с сыновьями Бернулли — Даниилом (портрет слева) и Николаем (потрет справа), которые тоже занимались математикой. (6)

Юный Эйлер написал несколько научных работ. «Диссертация по физике о звуке» получила благоприятный отзыв. В то время число научных вакансий в Швейцарии было невелико. Поэтому братья Даниил и Николай Бернулли уехали в Россию, где начинала создаваться Российская Академия наук; они обещали похлопотать там и о должности для Эйлера. В начале зимы 1726 года Эйлеру пришло письмо из Санкт - Петербурга: по рекомендации братьев Бернулли он приглашён на должность адъюнкта по физиологии с окладом 200 рублей. Эйлер провёл много времени в России, где внёс существенный вклад в российскую науку. С 1731 был избран академиком Петербургской Академии. Хорошо знал русский язык, а сочинения и учебники публиковал на русском. (6)

Тогда Эйлер подробно описывает свой метод решения некоторых задач при помощи кругов Эйлера. В 1741 году Эйлер пишет «Письма о разных физических и философических материях, к некоторой немецкой принцессе..», где упоминаются «круги Эйлера». Эйлер писал, что «круги очень подходят для того, чтобы облегчить наши размышления». (3)

Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли по-своему. Бернард Больцано использовал тот же метод, но с прямоугольными схемами. Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна. Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только. (1)

Вот несколько задач для решения, которых, удобно использовать круги Эйлера:

Задача 1.

У ребят из одной школы спрашивали об их домашних животных. 100 из них ответили, что у них дома есть собака и/или кошка. У 87 ребят была одна собака, а у 63 ребят - одна кошка. У скольких ребят есть и собака и кошка?

Решение:

Чтобы решить эту задачу, не используя круги Эйлера нужно подсчитать, сколько собак и кошек было у учеников. Для этого нужно сложить 87 и 63. 87+63=150 домашних животных. Учеников было всего лишь 100, а дробного числа домашних животных получиться не может. Значит если у каждого ученика 1 домашнее животное, остается еще 50 лишних. Следовательно, у 50 учеников 2 домашних животных. И так как в задаче указано, что ни у одного из учеников нет 2 кошек или 2 собак, то это значит, что у 50 учеников есть и кошка и собака.

Но этот способ долгий и подходит только для простых задач. Такую задачу намного удобнее решить через круги Эйлера.

Красным кругом изобразим множество обладателей собак, а синим множество обладателей кошек. Всего учеников было 100. Тех, у кого есть и кошка, и собака Х. Чтобы найти количество учеников, у которых только собака нужно из 87 вычесть Х. Так как всего учеников 100, мы получаем:

Х=50 учеников

Ответ: у 50 учеников есть и кошка и собака

Задача 2.

Однажды учеников спросили, кто из них любит математику, кому нравится русский язык, а кому физика. Оказалось, что из 36 учеников 2 не любят ни математику, ни русский, ни физику. Математика нравится 25 ученикам, русский язык- 11, физика - 17 ученикам; и математика, и русский- 6; и математика, и физика- 10; русский язык и физика - 4.

Сколько человек любят все три предмета?

Решение:

Изобразим 3 множества. Красное множество тех, кто любит математику, синие тех, кто любит русский язык, зеленое - физику.

Теперь впишем в множества количество элементов. 6 человек любят и русский и математику. Из них X человек любят еще и физику. Значит, только математику и русский любят 6-Х человек. Только математику и физику 10-Х, только русский и физику 4-Х человек. 25 человек любят математику. Но Х, 6-Х, 10-Х человек любят и другие предметы. Значит, только математику любят 25-(6-Х)-(10-Х)-Х= 25-6+Х-10+Х -Х=5+Х человек. Только русский любят 11-(6-Х)-(4-Х)-Х= 11-10+2Х-Х=1+Х учеников, только физику 17-(10-Х) -(4-Х)-Х= 17-14+2Х-Х= 3+Х.

Так как 2 человека не любят ни один из этих предметов, то:

3+Х+9+Х+1+Х+6-Х+10-Х+4-Х+Х=36-2

Ответ: 1 человек любит все три предмета

Задача 3.

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу природа? (4)

Решение :

По запросу человек было найдено 2100 тысяч страниц. 900 из них еще и о природе. Значит страниц только о человеке 2100-900=200 тысяч, а только о природе Х-900 тысяч. Получаем, что:

2100-900+Х-900+900=3400

2100-900+Х=3400

Х=2200 тысяч страниц

Ответ: по запросу природа будет найдено 2200 тысяч страниц.

Как видите Круги Эйлера - это полезное и важное открытие для математики в целом и для каждого из нас в частности. Круги Эйлера встречаются не только на экзаменах, но и нужны нам в повседневной жизни. Это интересная и необходимая вещь, о которой не стоит забывать.

Литература:

https://www.tutoronline.ru/blog/krugi-jejlera

https://ru.wikipedia.org/wiki/%D0%9A%D1%80%D1%83%D0%B3%D0%B8_%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0

http://sibac.info/shcoolconf/science/xvii/42485

http://www.jwy.narod.ru/logic/_04_eiler.html

https://ru.wikipedia.org/wiki/%D0%AD%D0%B9%D0%BB%D0%B5%D1%80,_%D0%9B%D0%B5%D0%BE%D0%BD%D0%B0%D1%80%D0%B4

При решении многих задач, связанных с множествами, незаменимым оказывается приём, основанный на использовании так называемых «кругов Эйлера». Эти диаграммы впервые появились в работах одного из величайших математиков в истории Леонарда Эйлера, который в течение продолжительного времени жил и работал в России и был членом Петербургской академии наук. Использование кругов Эйлера добавляет наглядности при решении сложных задач, делая многие вещи буквально очевидными. Предлагаю вам в этом убедиться самостоятельно на примере решения следующей задачи.

Пример решения задачи с помощью кругов Эйлера

Тут нужно понимать, что если сказано, что «42 человека используют метро», то это вовсе не означает, что кроме метро они не используют никаких других видов транспорта. Кто-нибудь из них может быть и использует. Может быть ещё какой-то один вид транспорта, трамвай или автобус. А может и сразу оба! Вопрос задачи как раз и состоит в том, чтобы посчитать людей, которые используют все три вида транспорта.

С первого взгляда даже непонятно, с чего начинать решение. Но если немного поразмыслить, становится ясно, что действовать нужно по следующему алгоритму. Будем стараться расписать всех людей (58 человек) через известные из условия данные. Нам известно, что автобус используют 44 человека. Прибавим к этому количество людей, которые используют метро. Их всего 42 человек. С помощью кругов Эйлера эту операцию можно изобразить наглядно в следующем виде:

То есть пока что мы имеем дело с выражением 58 = 44 + 42… Знак «…» означает, что выражение ещё не закончено. Проблема в том, что мы посчитали людей на пересечении этих кругов дважды. Соответствующая область на диаграмме выделена тёмно-зелёным цветом. Поэтому один раз их нужно вычесть. Это люди, которые пользуются автобусом и метро. Их, как известно, 31. То есть наше «неоконченное» выражение принимает вид: 58 = 44 + 42 — 31… И на диаграмме при этом пропадает тёмно-зелёный цвет:

Пока всё хорошо. Прибавляем теперь людей, которые ездят на трамвае. Таких людей 32. Выражение принимает вид: 58 = 44 + 42 — 31 + 32… Диаграмма с кругами Эйлера, в свою очередь, становится следующей:

К счастью в незакрашенной области как раз и находятся те люди, число которых нам нужно посчитать. Действительно, эти бедняги используют ежедневно все три вида транспорта для того, чтобы добраться до работы, ведь они находятся на пересечении всех трёх множеств. Обозначим количество этих бедолаг за . Тогда диаграмма примет следующий вид:

А уравнение станет следующим:

Расчёты дают . Это и есть ответ к задаче. Столько людей используют все три вида транспорта каждый день, чтобы добраться на работу.

Вот такое вот простое решение. Фактически, в одно уравнение. Просто удивительно, не правда ли?! А теперь представьте, как пришлось бы решать эту задачу без использования кругов Эйлера. Это было бы настоящее мучение. Так что в очередной раз убеждаемся, что любые методы визуализации чрезвычайно полезны при решении задач по математике. Используйте их, это поможет вам в решении сложных задач как на олимпиадах, так и на вступительных экзаменах по математике в лицеи и вузы.

Чтобы проверить, хорошо ли вы поняли решение данной задачи, ответьте на следующие вопросы:

Сколько человек используют только один вид транспорта для того, чтобы добраться до работы?
Сколько человек используют для этого ровно два вида транспорта?

Свои ответы и варианты решения присылайте в комментариях.

Материал подготовил , Сергей Валерьевич